| Springhead Users Manual |
 自由度関節の場合
自由度関節の場合PHJoint1DDesc |
||
double |
spring |
可動範囲下限 |
double |
damper |
可動範囲上限 |
double |
targetPosition |
可動範囲制限用バネ係数 |
double |
targetVelocity |
可動範囲制限用ダンパ係数 |
double |
offsetForce |
|
double |
fMax |
|
PHJoint1DIf |
||
double |
GetPosition() |
関節変位を取得 |
double |
GetVelocity() |
関節速度を取得 |
void |
SetSpring(double) |
|
double |
GetSpring() |
|
void |
SetDamper(double) |
|
double |
GetDamper() |
|
void |
SetTargetPosition(double) |
|
double |
GetTargetPosition() |
|
void |
SetTargetVelocity(double) |
|
double |
GetTargetVelocity() |
|
void |
SetOffsetForce(double) |
|
double |
GetOffsetForce() |
|
void |
SetTorqueMax(double) |
最大関節トルクを設定 |
double |
GetTorqueMax() |
最大関節トルクを取得 |
関節を駆動する力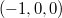 は次式で与えられます.
は次式で与えられます.
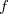 |
ここで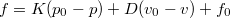 ,
,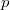 はそれぞれ関節変位と関節速度でGetPosition,GetVelocityで取得できます. その他の記号とディスクリプタ変数との対応は以下の通りです.
はそれぞれ関節変位と関節速度でGetPosition,GetVelocityで取得できます. その他の記号とディスクリプタ変数との対応は以下の通りです.
|
spring |
|
damper |
|
targetPosition |
|
targetVelocity |
|
offsetForce |
上の式はバネ・ダンパモデルとPD制御則の二通りの解釈ができます. 前者としてとらえるなら はバネ係数,
はバネ係数,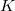 はダンパ係数,
はダンパ係数,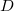 はバネの自然長,
はバネの自然長,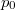 は基準速度となります. 後者としてとらえる場合は
は基準速度となります. 後者としてとらえる場合は はPゲイン,
はPゲイン,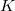 はDゲイン,
はDゲイン,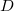 は目標変位,
は目標変位,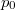 は目標速度となります. また,
は目標速度となります. また,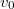 は関節トルクのオフセット項です. 上の式で得られた関節トルクは最後に
は関節トルクのオフセット項です. 上の式で得られた関節トルクは最後に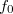 fMaxの範囲に収まるようにクランプされます.
fMaxの範囲に収まるようにクランプされます.
ヒンジと同様に,バネダンパモデル・PD制御を実現します. ボールジョイントの変位はクォータニオンで表されるため,目標変位targetPositionはクォータニオンで,目標速度targetVelocityは回転ベクトルで与えます.
=
PHBallJointDesc |
||
double spring & バネ係数 |
||
double damper & ダンパ係数 |
||
Quaterniond targetPosition & 目標変位 |
||
Vec3d targetVelocity & 目標速度 |
||
Vec3d offsetForce & モータートルク |
||
double fMax & 関節トルクの限度 |
||